本文尝试以量化分析的方法识别美国库存周期的构成、时变规律，并对未来走势进行预测。

通过对库存周期需求端和库存端进行傅里叶变换，我们发现需求端除了受库存周期的驱动外，还受到投资周期以及地产周期的影响；库存端则主要受到自身库存周期以及投资周期的影响，这说明库存更多是企业和供应链对中短期供需状况和预期作出的反应。

随着技术进步和政策调整，库存周期的主导频率和幅度可能会发生潜在变化。我们引入小波变换探究库存周期的时变性，从时变特征看，尽管不同时间影响库存端和需求端的周期长度不同，但是周期仍然具有一定持续性，这种持续性给我们提供了预测的空间。

我们采用小波变换滚动识别周期+高斯滤波拟合对需求端和库存端进行预测。从滚动预测的胜率看，需求端和库存端对未来的预测胜率在65%左右；从拐点误差来看，若未来库存周期预期出现拐点，则该模型与需求端最近拐点的平均偏离为3.38个月，库存端平均偏离3.2个月。

站在2025年8月预测，未来12个月美国库存周期将完成主动去库存到被动去库存的转换，即完成第二库存周期需求下行阶段，并进入第三库存周期需求复苏期。美债通常在库存周期需求下行期表现较好，待进入第三库存周期需求复苏期，特别是主动补库期，收益表现将欠佳。

宏观经济的运行蕴含着周期波动之美，从供需平衡驱动的库存周期（3-5年），到设备更替、资本支出主导的投资周期（7-11年），再到人口增长、城市化进程塑造的地产周期（15-30年），不同周期相互交织、彼此共振，伴随着资产价格不同形式的波动。若能从周期运行的规律中窥见一二，便能自上而下识别投资交易机会、防范潜在风险。

库存周期是最短的经济周期，并且对大类资产的中短期波动有显著影响。本文从库存周期切入，尝试以量化方法识别美国库存周期的构成、时变规律并对未来走势进行预测。

一、库存周期划分

库存周期通常根据需求和库存的上下行情况划分为四个阶段：被动去库存（需求上、库存下）、主动补库存（需求上、库存上）、被动补库存（需求下、库存上）、主动去库存（需求下、库存下）。

指标选取上，考虑到指标的领先性、公布时点、是否易出现极端值等因素，我们选择美国ISM制造业PMI新订单、密歇根大学消费者信心指数作为需求端代理指标，选择美国ISM制造业PMI自有库存作为库存端代理指标。

指标构建上，对于需求端，我们将美国ISM制造业PMI新订单、密歇根大学消费者信心指数经过z-score标准化之后等权合成，并使用低参hp滤波[1]（λ=6）提取趋势项；对于库存端，直接对美国ISM制造业PMI自有库存z-score标准化后低参hp滤波去噪。

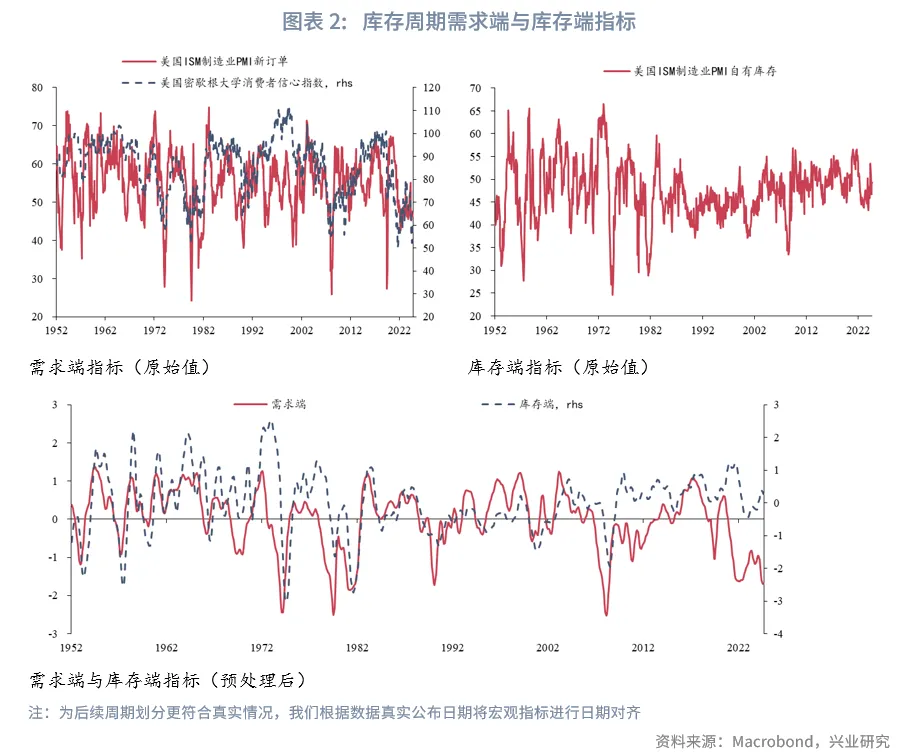
根据需求端和库存端的上下行情况，我们可以划分自1952年12月以来美国的库存周期。从不同阶段出现次数来看，被动去库存出现24次，平均持续4.86个月；主动补库存出现28次，平均持续10.38个月；被动补库存27次，平均持续7.7个月；主动去库存26次，平均持续10.33个月。从各阶段平均持续时间来看，被动去（补）库存阶段相对主动去（补）库存阶段持续时间较短，这种时间不对称性反映了经济系统中成本调整、预期形成机制和供应链刚性的深层规律。被动阶段往往是市场倒逼下的快速调整，而主动阶段是企业决策惯性的延续。

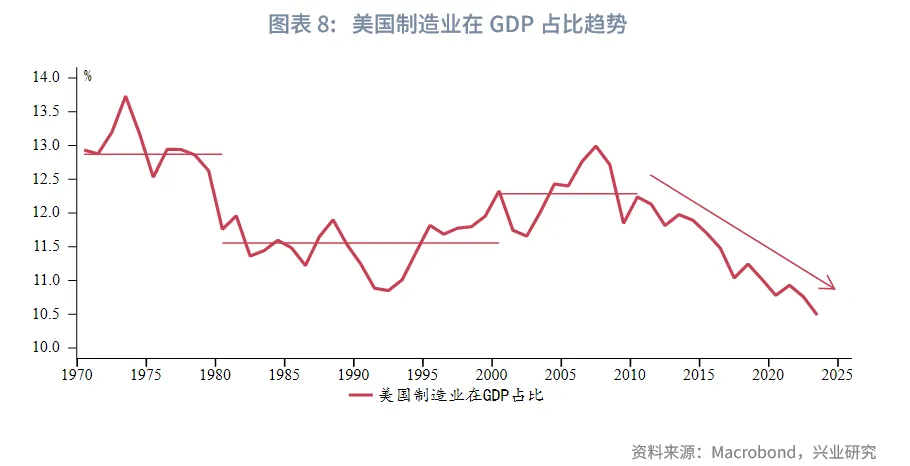
从当前阶段看，2024年3月至2025年6月，美国被动补库存阶段已持续16个月，这一异常现象是多重因素叠加作用的结果。核心驱动因素包括：疫情后企业采购策略变化，倾向于保持更高的库存水平；受到人口结构、产业政策、财政支出等因素共同影响，美国经济总体保持韧性；特朗普上任后高关税预期引发的“抢进口”带来库存水平提高。值得注意的是，当前库存周期的演变已不再单纯遵循周期规律，而呈现出“地缘政治+周期规律”的新特征。

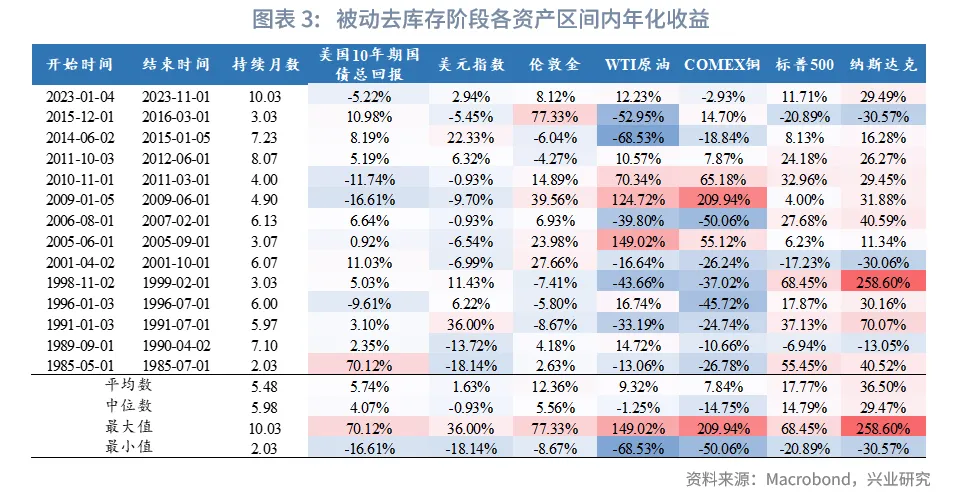
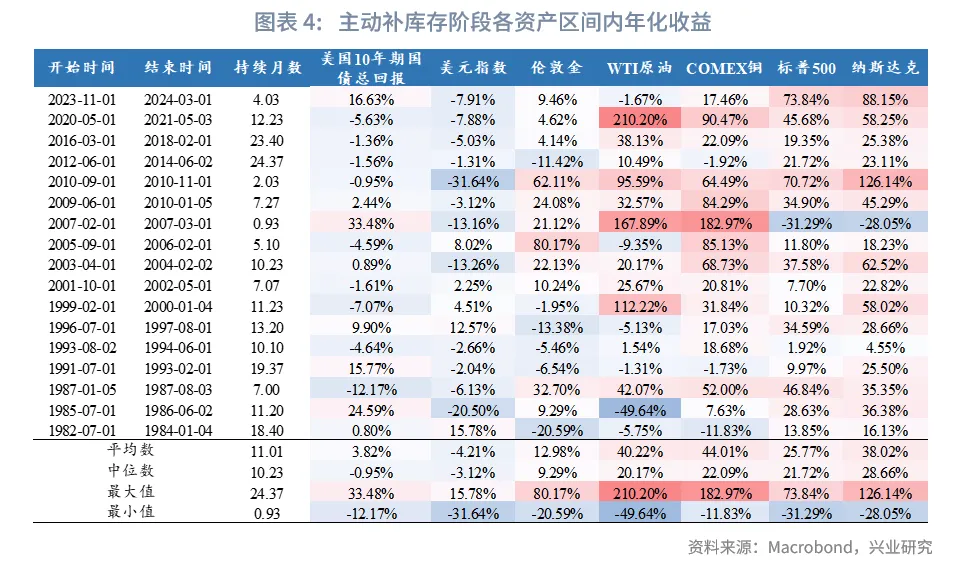
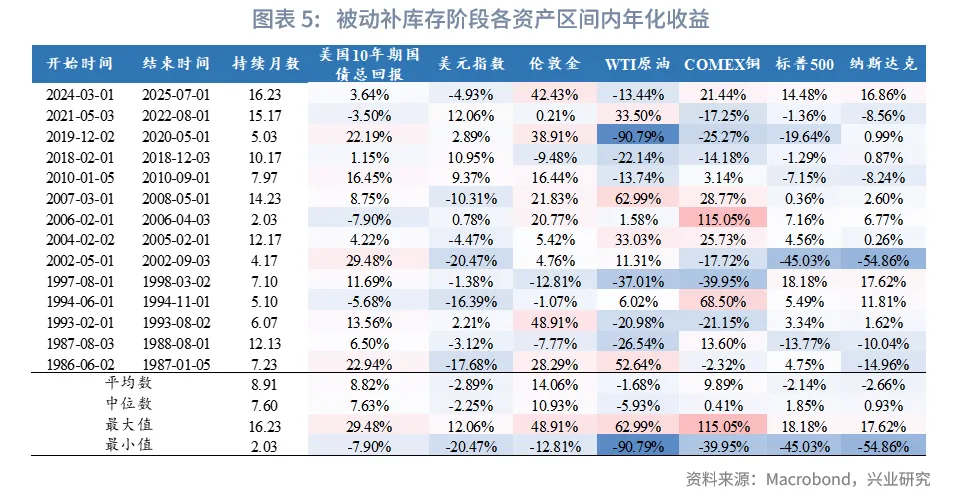
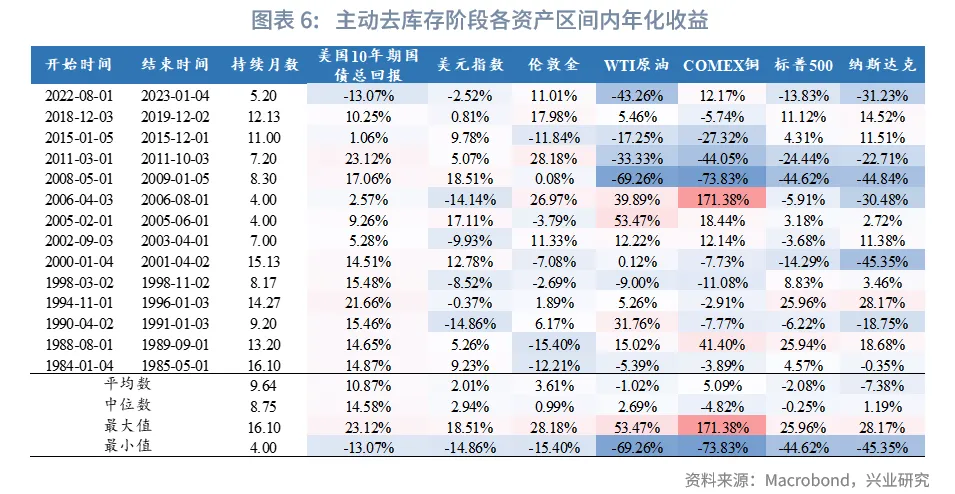
从1982年以来不同阶段大类资产的收益水平来看，在被动去库阶段，美股收益较优；在主动补库存阶段，美股、原油、铜、黄金收益较优，美债、美元收益较低；在被动补库存阶段，美债、黄金表现较优，原油、美股收益较低；在主动去库存阶段，美债收益较优，美股、原油收益较低。

二、库存周期识别

直观观测上，库存周期的长度普遍在3-5年，而投资周期、地产周期等中长周期的存在同样会驱动库存周期的变动，本章我们主要对驱动库存周期的主要周期进行定量测算并对其时变特性进行探讨。

2.1 库存周期长度识别

如何识别不同长度周期对库存周期的影响？傅里叶变换是一个不错的选择，傅里叶变换的核心是将一个复杂的信号拆解成多个简单的正弦波，被广泛的应用于物理学和通信领域。

傅里叶变换公式如下：

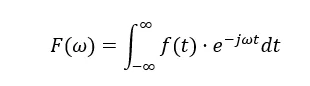
其中f(t)是原始信号，e^-jωt是复指数函数，可以看作一个频率为的ω探针，将f(t)与e^-jωt相乘并积分的过程可以看作计算f(t)与频率ω的信号相似度，频率F(ω)越接近，的值越大。

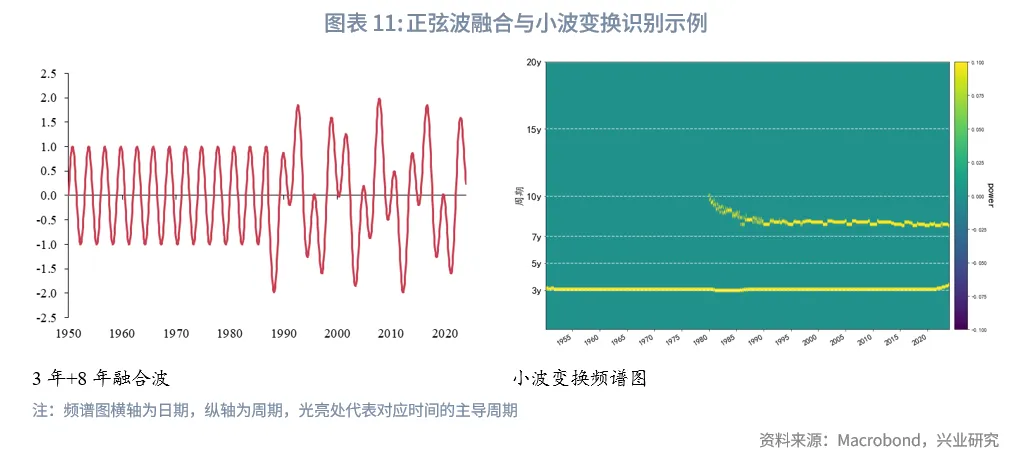
举例来看，我们将2个周期分别为3年、8年的正弦波相加得到融合波，并对融合波进行傅里叶变换，频谱图在36/96个月均出现了峰值，说明融合波是由这两个周期波共同作用产生。

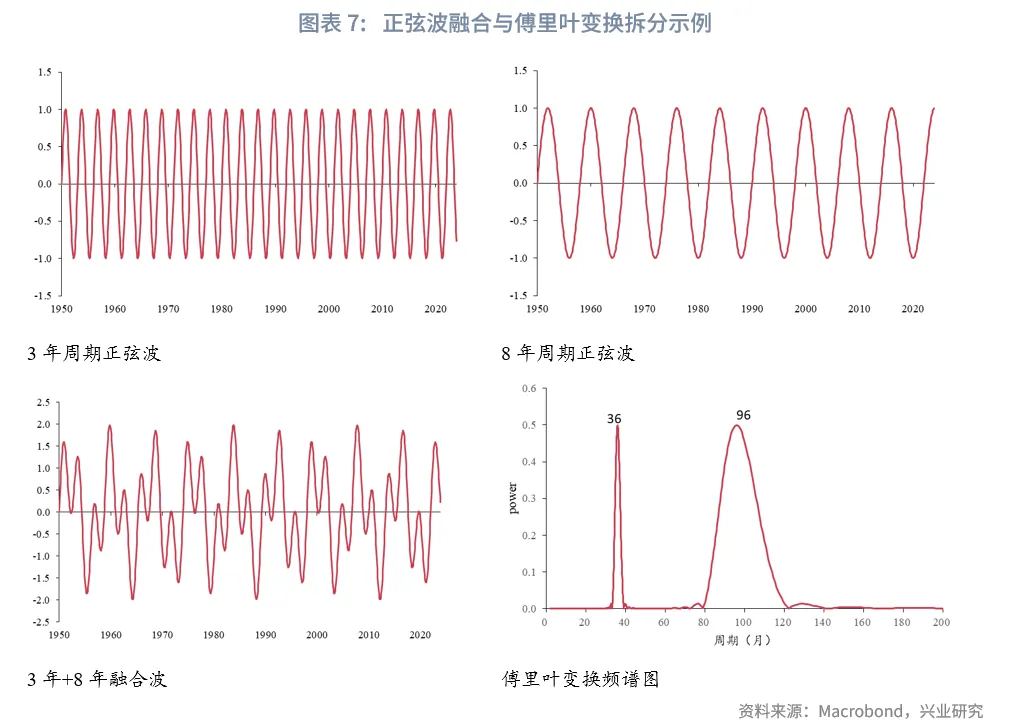
类似地，我们对库存周期需求端和库存端分别进行傅里叶变换。考虑到1980年以来，美国的“制造业空心”趋势改变了库存周期的运行逻辑，库存周期逐渐由生产主导转向消费主导。我们将时间区间分成两段，一段为1952-1980年，另一段为1980年至2025年7月。

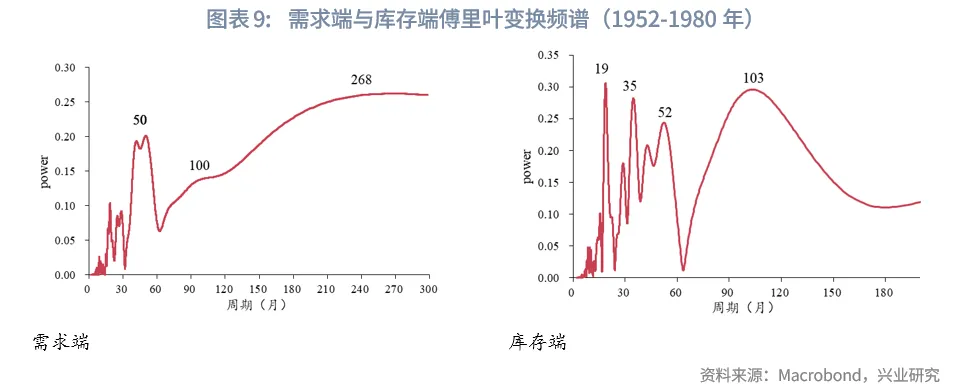
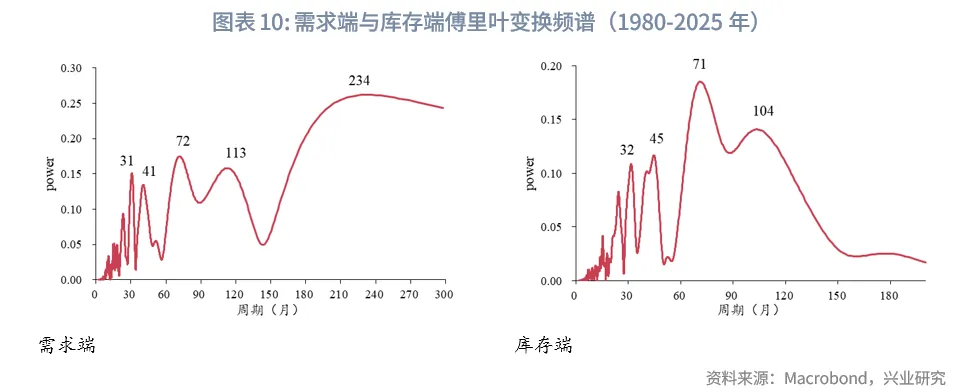
根据傅里叶变换结果，1952-1980年，需求端主要受到50、100、268个月的周期影响，库存端主要受到19、35、52、100个月的周期影响；1980-2025年，需求端主要受到31、41、72、113、234个月的周期影响，库存端主要受到32、45、71、104个月的周期影响。

整体可以看出需求端除了受到库存周期的短周期驱动外，还受到投资周期、地产周期等更长周期的影响。库存端则主要受到库存周期以及投资周期的影响，这说明长期因素（如人口、城市化驱动的房地产周期）对库存水平本身的直接影响相对较弱，库存更多是企业和供应链对中短期供需状况和预期作出的反应。

相较之下，1980年之前，美国经济以制造业主导，设备更新与产能扩张是核心驱动力，需求端本质是生产派生型需求，库存端的短周期主要反映了当时的生产节奏。1980年之后随着美国经济逐渐转为消费型主导，全球化进程推动需求端与全球供应链同步，使得中周期进一步凸显（频谱图中72、113个月的周期振幅增强）；伴随着信用卡普及率以及股票参与率的提升，需求端与金融周期进一步绑定，使得需求端短周期得到强化（频谱图中31、41个月的周期振幅增强）。而库存管理范式的变革使得库存逐渐成为需求传感器而非生产缓冲器，表现为二者均受到32、43、72、109个月左右的周期驱动（需求端与库存端临近周期取平均值）。

2.2 库存周期时变性探讨

傅里叶变换能够帮助我们在较长时间内识别库存周期的驱动频率，但是其无法及时反映周期长度的变化。因此我们引入小波变换来进一步探究库存周期的时变性。

小波变换与傅里叶变换的主要区别是探针的不同，傅里叶变换是随时间变化而频率固定的探针，适合全局识别，小波变换则是在时间上可伸缩的探针。小波变换的主要优势是能够识别非平稳序列局部时间段的周期。

小波变换公式如下：

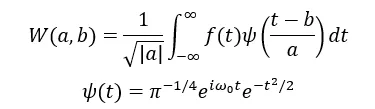
其中，a是缩放因子（控制小波的“窗口宽度”），b是平移因子（控制小波在时间轴上的位置），ψ(t)是满足容许条件的母小波函数。通过调整a和b，小波变换能够动态平衡时间分辨率和频率分辨率：对于高频成分（如库存周期中的短期波动）：使用小尺度（a→0），小波窗口变窄，时间分辨率高，但频率分辨率低。低频成分（如库存周期的长期趋势）：使用大尺度（a→∞），小波窗口变宽，频率分辨率高，但时间分辨率低。

举例来看，我们将2个周期分别为3年、8年的正弦波相加得到融合波并通过小波变换识别周期，其中8年正弦波只在后半段时间出现。从频谱图中的光亮处可以看出，小波变换能较为准确的识别出不同时间段对应的周期，只是小波函数的局限性导致了其在序列两端的周期识别能力有所降低。

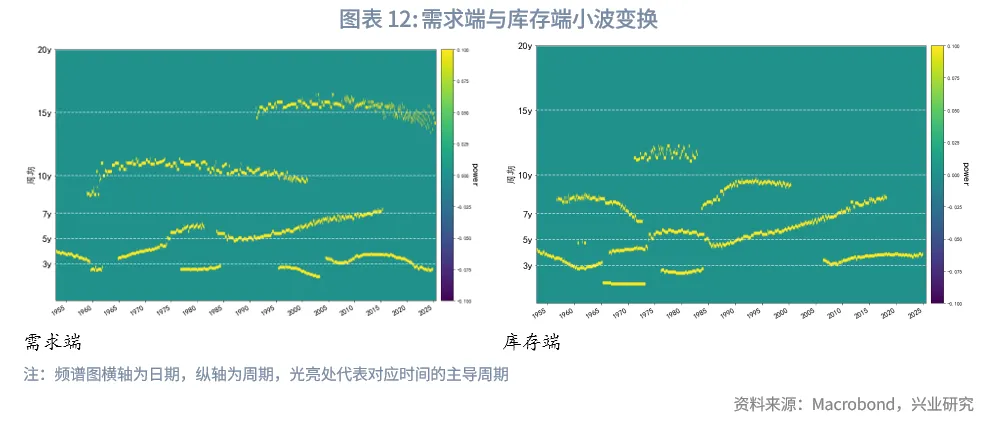
类似地，我们对1952年12月到2025年7月的需求端和库存端分别进行小波变换。由于小波变换在长周期识别上可能会出现能量分散，我们只识别20年以内的周期。从时变特征来看，尽管不同时间影响库存端和需求端的周期长度不同，但是周期变动仍然具有一定持续性。如需求端在1960年到2000年左右受到较为稳定的10年左右周期驱动（投资周期）。1990年到2020年间受到稳定的3年、15年左右周期驱动，与傅里叶变换结果互相印证。2020年疫情后，强劲的地产市场依然对需求端有显著影响。库存端自2010年以来也受到较为稳定的4年左右周期驱动。这种持续性给我们提供了预测的空间。

三、库存周期预测

前文中我们通过全域傅里叶变换和小波变换探究了库存周期的变与不变。若能用已知的周期波拟合出需求端和库存端的走势，再根据单个周期波的可预测性，便能够对需求端和库存端的整体趋势进行预测。

本章我们首先在全域用固定周期的高斯滤波拟合需求端和库存端，查看拟合效果；而后根据小波变换滚动确定最新周期，并用最新周期的高斯滤波对需求端和库存端走势进行预测。

3.1 库存周期全域拟合

鉴于1980年后美国经济结构的深刻变化，我们主要以1980年后的数据为样本开展后续研究。根据2.1节傅里叶变换的结论，1980年以来需求端主要受到31、41、72、113、234个月的周期影响，库存端主要受到32、45、71、104个月的周期影响。二者并不是完美重复的正弦波叠加，它们可能在某些时段变强、某些时段变弱，甚至中间有间歇。因此我们考虑用高斯滤波进行拟合。高斯滤波的核心优势在于：一是，它可以“锁定”某个中心周期，只让这个周期附近的信号通过（比如中心周期是45个月，我们允许让40到50月的周期通过）。二是，高斯窗口允许我们局部加权，适应周期强度的变化，从而处理周期的“衰减”和“增强”。这两个优势使得高斯滤波既具有正弦波的可预测性，又具有正弦波没有的灵活性。

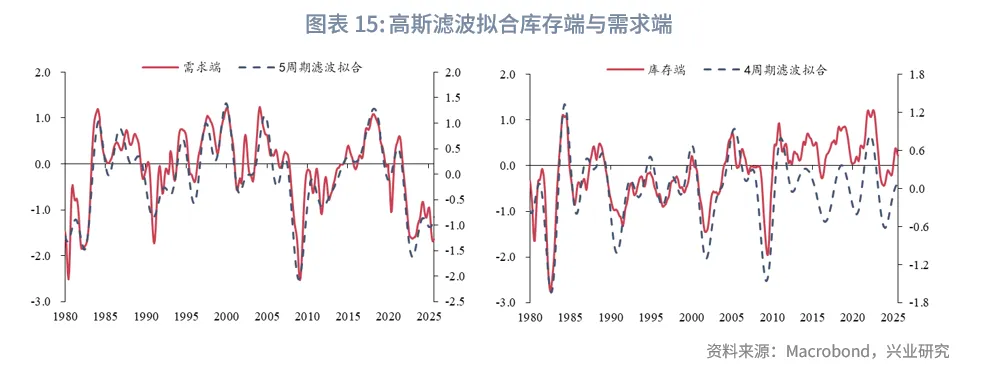
根据傅里叶变换结果对1980年以来需求端和库存端构建对应周期的高斯滤波。从高斯滤波的形态来看，短时间内高斯滤波与正弦波形态接近，同时高斯滤波的振幅反映了对应周期对指标的影响程度。从图中可以看出2000年以来41~45个月的周期分别对需求端和库存端产生较为稳定的影响。

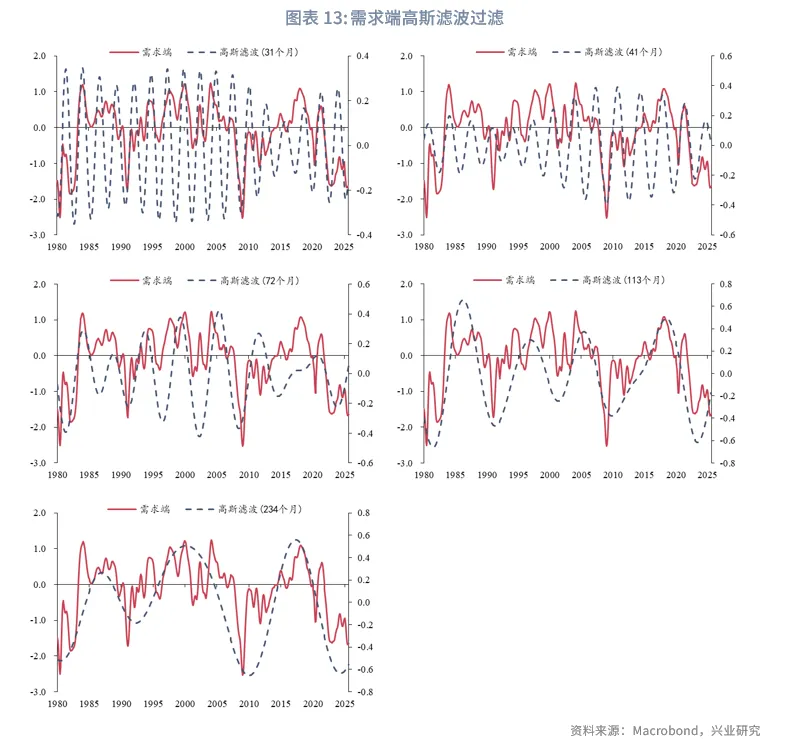
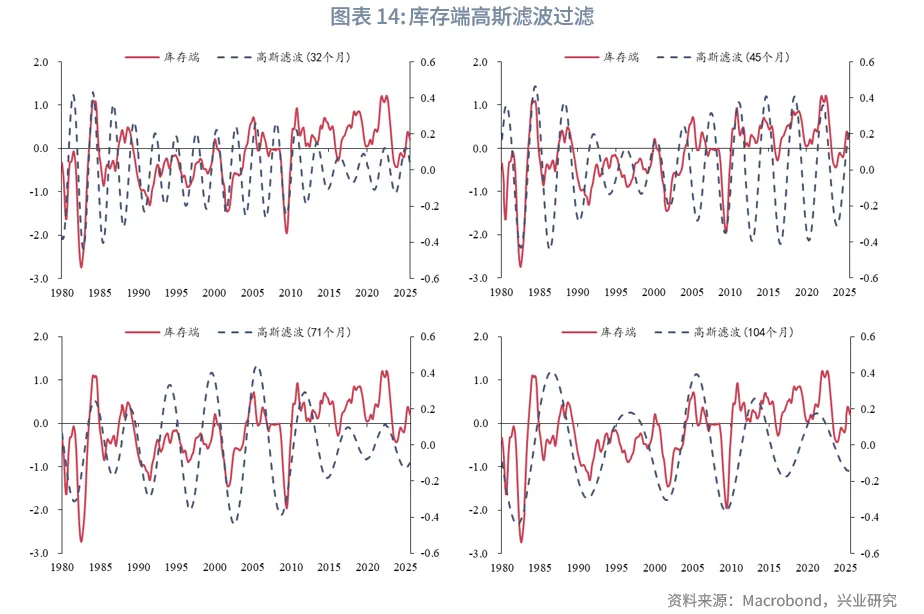
若分别以需求端和库存端为因变量，对应不同周期的高斯滤波为自变量，构建OLS回归模型，需求端拟合优度为85.56%，库存端拟合优度为55.49%，整体拟合效果较优。

3.2 库存周期滚动预测

为了更好地适应宏观环境变化，我们采用滚动拟合+合理外推的方式对需求端和库存端进行预测，整体分为三步。

（1）小波变换确定主要周期

滚动过去20年需求端（库存端）进行小波变换。由于小波变换在每个月都能动态识别出影响最大的n个周期，从及时性、减小误差、防止过拟合等维度考量，周期选择上我们遵循以下原则：由于最后一年数据误差较大，剔除最后一年小波变换的结果；一轮库存周期大约5年，因此取过去5年每个月的前2周期的中位数作为主要周期；由于只进行短期预测，要求主要周期不大于15年；为了保证周期稳定存在，近5年主要周期存续时间不低于2年；为了防止过拟合，若主要周期之间相隔小于2年，只保留强度更高的周期。

（2）滚动拟合库存周期

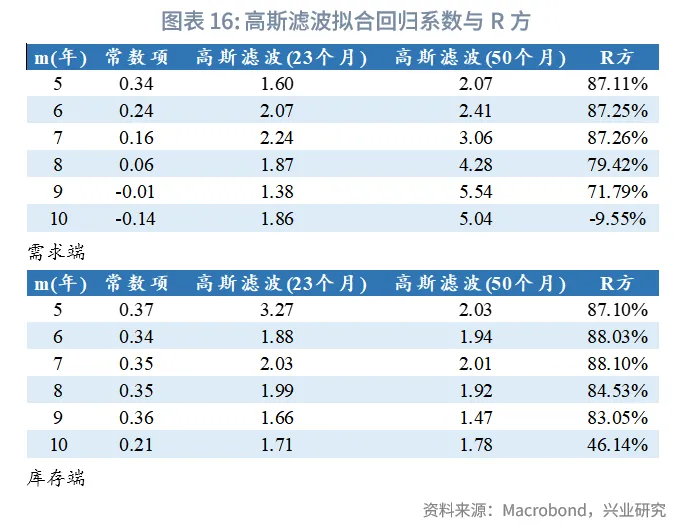
由于不同起始时间的高斯滤波有所差异，因此，每个月我们分别滚动过去m年的数据（m=5、6、7、8、9、10）构建主要周期的高斯滤波，并选择最近5年R方最优的参数m及其对应的回归系数。

（3）高斯滤波外推一年

将最近一个周期的高斯滤波当成正弦波进行拟合，并根据正弦波的性质合理外推一年。

我们先检测模型的样本外预测能力。以2019年1月为起点预测需求端、库存端未来走势为例，根据滚动过去20年小波变换结果，确定近五年需求端前2主周期中位数分别为45个月、76个月，库存端分别为个20个月、46个月；接着以过去m年数据构建高斯滤波并回归拟合，回归结果显示在m=7年时需求端和库存端的拟合R方最大；因此分别将2个主周期外推一年，并带入m=7年时的回归系数，即可得到未来一年的走势预测。

从预测结果来看，模型预测需求端和库存端在未来12个月有下行趋势，与指标样本外变动方向一致，幅度上可能会有较大偏差，因此本模型主要目标是给出方向上的参考建议。

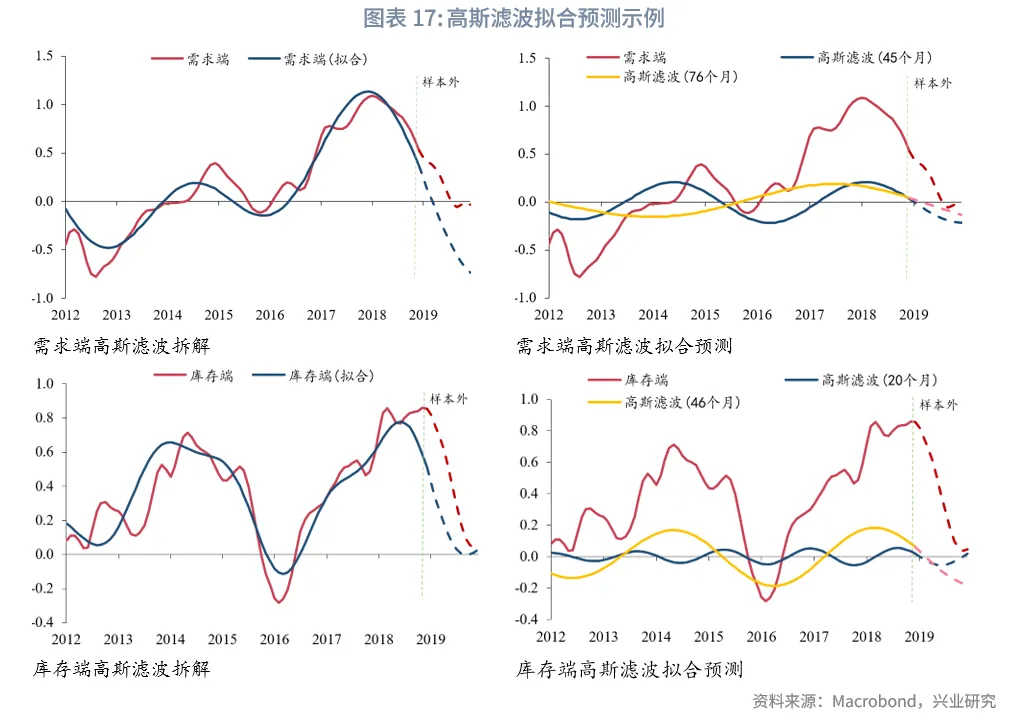
接着我们对模型的效果整体效果进行回测，样本区间为1952年12月-2025年7月，每个月对未来1年数据进行预测，验证其对未来1个月、3个月、6个月、12个月变动方向预测的胜率。

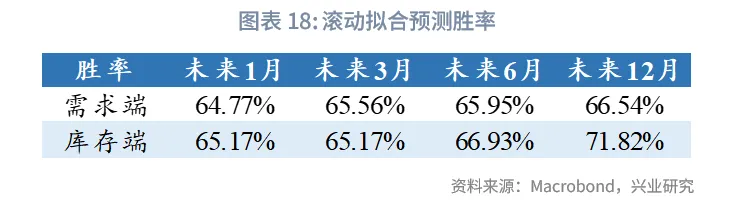
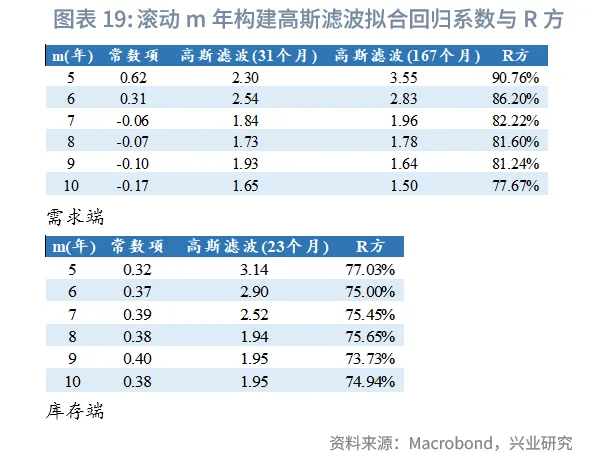
从拟合效果来看，需求端在滚动样本内平均R方为82.02%，库存端平均R方为81.70%，与全样本拟合相比，滚动拟合只用到了前2个主周期便达到了较好的拟合效果；从滚动预测的胜率来看，需求端和库存端对未来的预测准确度在65%左右，预测效果较优；从拐点误差来看，若未来一年库存周期出现拐点，则该模型与需求端最近一个拐点的平均偏离为3.38个月，库存端拐点平均偏离3.2个月。

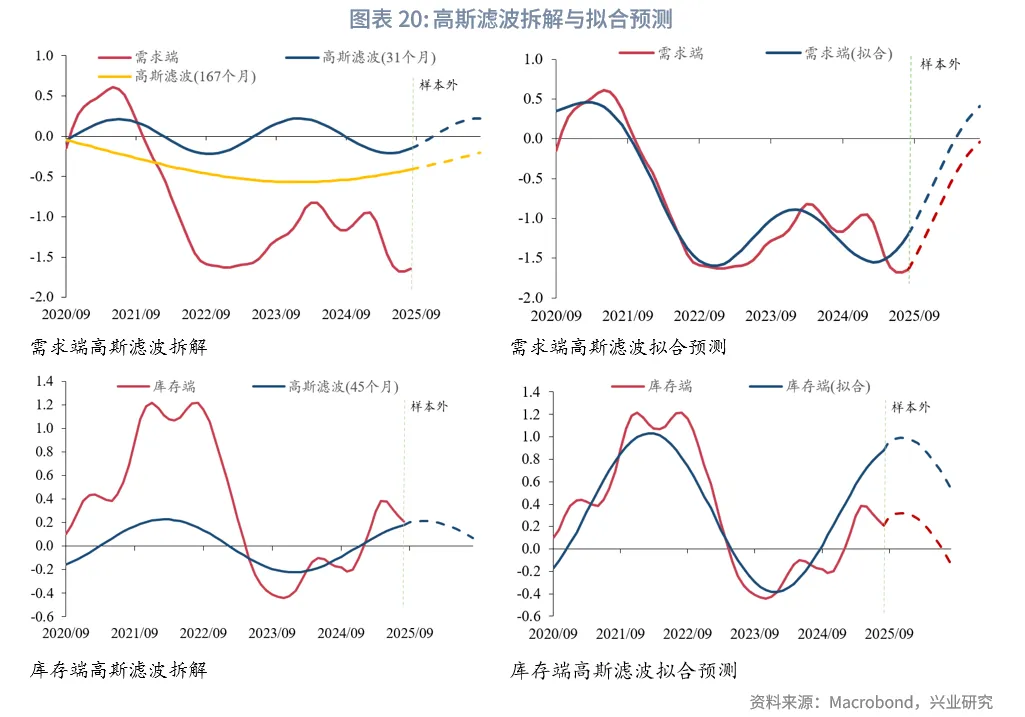
若我们站在2025年8月，对未来1年需求端和库存端走势进行预测，根据滚动过去20年小波变换结果，确定近五年需求端前2主周期中位数分别为31个月、167个月（约14年），库存端为45个月；接着以过去m年数据构建高斯滤波并回归拟合，回归结果显示在m=5年时需求端和库存端的拟合R方最大；因此分别将主周期外推一年，并带入m=5年时的回归系数，可以看出未来12个月需求端有上行趋势，库存端有下行趋势。预测值的方向具有较强的参考意义，但幅度可能和实际值存在较大偏差。

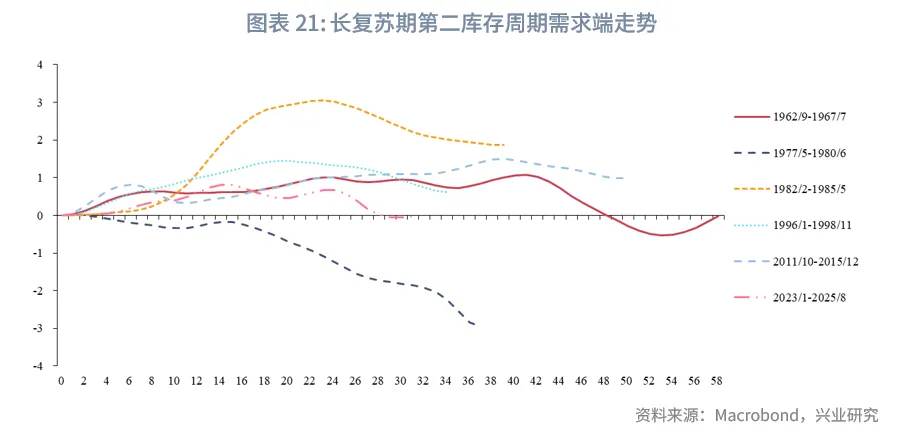
通过对比了长复苏期（包含3个库存周期）的第二库存周期需求端走势，目前可能和1962~1967年、2011~2015年类似，需求端在经历了快速下行后暂时进入平台期，期间需求可能有所反弹，此后需求再度下行，完成最后的主动去库存后进入下一轮库存周期。结合高斯滤波的预测，可以预判未来12个月美国库存周期将完成主动去库存到被动去库存的转换。

在实际环境下，量化模型的整体胜率受到周期稳定性的影响，若某个突发事件导致周期长度出现系统性的变化，则我们用小波变换识别出的周期可能会出现偏离，导致模型失效。因此使用模型时应关注近一段时间主要周期是否稳定，是否有重大影响事件可能影响库存周期。

此外，模型中我们通过R方选择最优滚动期数构建高斯滤波可能并不是最好的选择，有时拟合优度高并不意味着拐点匹配更优。并且较短的滚动时长可能在对较长主周期构建高斯滤波时产生误差，但是由于我们的目标是预测短周期，这是我们不得不做的权衡。在实际应用层面，我们可能需要结合自己的主观能动性来进一步提高模型胜率，观察不同滚动期m年的高斯滤波，选择拐点匹配较优且R方较优的结果进行预测。

注：

[1]低参hp滤波在边缘处滞后较小，控制在1个月左右，也较少有高参hp滤波边缘处不稳定情况，主要起到去噪声作用。

来源：兴业研究公众号